PropLogic is a Haskell package for propositional logic. It also contains a standalone executable of the same name, which is able to run a small collection of the functions defined in the package. Most of them are Prime Normal Form converters of some sort.
For example, consider the spdnf function that returns the Simplified Prime Disjunctive Normal Form of a given propositional formula
$ ./PropLogic spdnf "[-[-x * y] * [-y + z] * --[-x + z] * [z + y + z]* true]" [[x * z] + [-y * z]]
i.e. PropLogic applies spdnf on [-[-x * y] * [-y + z] * --[-x + z] * [z + y + z] * true] and returns its unique equivalent Prime Normal Form, namely [[x * z] + [-y * z]].
The power of a normalizer like spdnf and its relatives first of all lies in the fact that it solves all traditional problems of propositional logic: Need to know if a formula is satisfiable? Need to know if two formulas are equivalent? All this is immediately answered with spdnf: the example input is satisfiable, because the result is not false, and it is not valid, because the result is not true.
Another feature of our prime form normalizers lies hidden in the underlying algorithms: they are fast. In a straight-forward, traditional, or default fashion, the mentioned problems are of exponential complexity and the computational costs to solve them explode. The PropLogic implementations however should be feasible for input of any size.
The second part of this introduction contains some data that translate "fast" into real numbers of seconds on a current standard computer.
The PropLogic package is written in the Haskell programming language. But no prior understanding of Haskell is required to handle the command or this document. It is written also for users that are just looking for a tool for solving propositional logical problems. In particular, it can be used as a fast SAT-solver.
For a detailed description of the installation see [Inst]. We give a quick and dirty version of the installation process here, which enables us to run the program.
PropLogic.exeinto a working directory. Start the terminal window (DOS command) and navigate (with
cd) to that place.
If you then run, say
PropLogic helpyou should find out that it works.
PropLogic-0.9.tar.gzinto an appropriate working directory. Extract the archive file with
$ tar -xvf PropLogic-0.9.tar.gzchange to the newly created subdirectory with
$ cd PropLogic-0.9and compile with
$ ghc --make -o PropLogic Main.hsThat should do it. Now check
$ ./PropLogic helpto confirm that everything works fine.
Note, that we follow a common convention to use $ as the standard shell (or DOS) prompt to indicate the user input.
When we write
$ PropLogic pdnf "[p <-> [-q + r]]" [[-p * q * -r] + [p * -q] + [p * r]]
then this means that we input PropLogic pdnf "[p <-> [-q + r]]" and we obtain the result [[-p * q * -r] + [p * -q] + [p * r]].
Unix-like systems however will not look in the working directory for the PropLogic command by default and it needs to be enforced to do so with the prefix ./ for the working directory. In other words, we have to modify the previous input line to
$ ./PropLogic pdnf "[p <-> [-q + r]]"
We continue this habit in the examples below.
Windows user should remember however to omit the prefix and replace the previous line by something like
C:\working\directory> PropLogic pdnf "[p <-> [-q + r]]"
where PropLogic may also be written proplogic, as Windows is case-insensitive in this respect.
The rules for the construction of formulas are represented by the following table.
| Syntax of propositional formulas (in fancy notation) | ||
|---|---|---|
α |
for every atom α |
atomic formula |
false |
zero or false value | |
true |
unit or true value | |
-φ |
for every formula φ | negation |
[φ1 * ... * φn] |
for all formulas φ1, ..., φn with n≥0 |
conjunction |
[φ1 + ... + φn] |
for all formulas φ1, ..., φn with n≥0 |
disjunction |
[φ1 -> ... -> φn] |
for all formulas φ1, ..., φn with n≥0 |
subjunction |
[φ1 <-> ... <-> φn] |
for all formulas φ1, ..., φn with n≥0 |
equijunction |
where an atom &alpha is any nonempty sequence of letters and digits, except for the keywords true and false.
|
||
Note, that
five example atoms (or atomic formulas) are given by
halloWorld 123 x tea4two 1and2and3
and two example formulas are given by
-[x + y + -[x * z] + [x -> y] + false + [-x + y]] [x <-> --x <-> [y * z] <-> [y -> true -> z]]
Con-, dis-, sub- and equijunctions are multiary or n-ary, i.e. they may have any number of arguments. A unary conjunction, i.e. a conjunction of only one formula phi is written [* phi]. The nullary conjunction is [*]. The same holds of the other junctors, although one usually doesn't need these cases.
The outer brackets [...] around the n-ary junctions are mandatory. That disambiguates the parsing of formulas and makes any
preference rules obsolete.
The notation here is called "fancy" because it is different from the "pure" notation, which is the real Haskell data type in the package implementation. In our context here however, we will only be dealing with the fancy version.
You will probably be familiar with the notion of a Disjunctive Normal Form (or DNF) and the Conjunctive Normal Form (or CNF).
A DNF is a disjunction of literal conjunctions, where a literal is either an atomic formula, or a negated atomic formula. For example,
[[-v * -w * x * -y * -z] + [v * w * -x] + [v * -x * z] + [-x * y]]
Our definition of a DNF also requires each literal conjunction to be a Normal Literal Conjunction (or NLC) in the sense that the atoms its literals are in a strict ascending order. For example, the second literal conjunction [v * w * -x] is a NLC, because v < w < x.
Similarly (or dually, as it is called in the context of boolean algebras), a CNF is a conjunction of Normal Literal Disjunctions (or NLDs), i.e. disjunctions of literals with atoms in a strict ascending order. An example CNF is say
[[-1 + -2 + 3 + -4 + -5] * [1 + 2 + -3] * [1 + -3 + 5] * [-3 + 4]]
In the sequel, we write <=> for the usual equivalence relation and => for the subvalence (or consequence or entailment relation) on formulas.
For example, --x <=> [x * true] and [x * y] => x are two true statements.
φ has an equivalent DNF Δ and an equivalent CNF Γ.
γ = [λ1 * ... * λk] be a NLC and Δ = [γ1 + ... + γn] a DNF.
We say that
γ is a factor of Δ, if γ => Δ.
γ is a prime factor of Δ, if γ is a factor of Δ and there is no other different factor γ of Δ with γ => γ' => Δ. In other words, if we delete any of the λi in γ, then the resulting NLC γ' = [λ1 * ... * λi-1 * λi+1 * ... * λk] is no longer a factor of Δ.
Δ is a Prime DNF or PDNF, if the components γ1, ..., γn are exactly the prime factors of Δ and if γ1 < ... < γn (where < is a standard linear order on NLCs).
δ = [λ1 + ... + λk] be a NLD and Γ = [δ1 * ... * δn] a CNF.
We say that
δ is a cofactor of Γ, if Γ => δ.
δ is a prime cofactor or coprime of Γ, if δ is a cofactor of Γ and there is no other different cofactor δ' of Γ with Γ => δ' => δ.
Γ is a Prime CNF or PCNF, if the components δ1,...,δn are exactly the coprimes of Γ and if δ1 < ... < δn (where < is a standard linear order on NLDs).
For example, [x * -y * -z] is a factor of the DNF [[x * -z] + [y * z]], because
[x * -y * -z] => [[x * -z] + [y * z]]
But it is not a prime factor, because [x * -z] is also a factor and
[x * -y * -z] => [x * -z] => [[x * -z] + [y * z]]
It is not possible to delete any more literals from [x * -z], the NLCs [* x] and [* -z] are no factors of the given DNF anymore, and that makes [x * -z] a prime factor.
Alltogether, there are three prime factors of [[x * -z] + [y * z]], namely [x * y], [x * -z] and [y * z]. Their disjunction
[[x * y] + [x * -z] + [y * z]]
is a PDNF.
(The three prime factors in this PDNF are properly ordered, i.e.[x * y] < [x + -z] < [y + z]. But we don't bother with the details of a proper definition for this linear order < on the NLCs.)Important is however, that this PDNF [[x * y] + [x * -z] + [y * z]] is equivalent to the original DNF. And that is a general fact:
φ holds:
Δ equivalent to φ.
This is called the PDNF of φ and denoted by
pdnf(φ).
Γ equivalent to φ.
This is called the PCNF of φ and denoted by
pcnf(φ).
The PropLogic package provides two Haskell functions [HNota]
pdnf :: (Ord a) => PropForm a -> PDNF a pcnf :: (Ord a) => PropForm a -> PCNF a
that return these normal forms of given propositional formulas (based on a linearly ordered atom type a).
From the command line, we can call these two functions with
$ ./PropLogic pdnf PROPFORM $ ./PropLogic pcnf PROPFORM
respectively, where PROPFORM is a propositional formula in fancy notation and wrapped in double quotes.
For example
$ ./PropLogic pdnf "[[x * -z] + [y * z]]" [[x * y] + [x * -z] + [y * z]]
$ ./PropLogic pcnf "[[x * -z] + [y * z]]" [[x + y] * [x + z] * [y + -z]]
$ ./PropLogic pdnf "[x -> y -> x]" [[-x * -y] + [x * y]]
The formal definition of DNFs and CNFs necessarily implies nullary and unary junctions like [*] and [+ x]. But most users would prefer a simplified version, as we call it. For example, one would rather write
[[x * y] + -z + v] instead of [[x * -y] + [* -z] + [* v]] [x * y * z] instead of [[+ x] * [+ y] * [+ z]] true instead of [+ [*]] true instead of [*]
etc. [SimpRules]. These abbreviated formulas are no DNFs and CNFs anymore in the strict formal sense. We call them simplified PDNFs and PCNFs or SPDNFs and SPCNFs, respectively. Accordingly, we have two command options
$ ./PropLogic spdnf PROPFORM $ ./PropLogic spcnf PROPFORM
to generate these slightly modified results. For example
$ ./PropLogic pcnf "[[x * -z] + [y + z]]" [* [x + y + z]] $ ./PropLogic spcnf "[[x * -z] + [y + z]]" [x + y + z]
$ ./PropLogic pdnf "[[x * -z] + [y + z]]" [[* x] + [* y] + [* z]] $ ./PropLogic spdnf "[[x * -z] + [y + z]]" [x + y + z]
$ ./PropLogic pdnf "[[x -> y] <-> [-x + y]]" [+ [*]] $ ./PropLogic spdnf "[[x -> y] <-> [-x + y]]" true
$ ./PropLogic pcnf "[x <-> -x]" [* [+]] $ ./PropLogic spcnf "[x <-> -x]" false
Most people would probably prefer to use these simplified versions in practice.
Each of these functions pdnf, pcnf, spdnf and spcnf is a canonical normalizer or canonizer for the equivalence relation <=> on propositional formulas in the sense that (1.) every formula is equivalent to its canonization and (2.) two formulas are equivalent if and only if their canonizations are identical.
We can exploit this property of canonizers for the solution of the traditional problems of propositional logic, e.g. the question, if a formula is satisfiable. So in particular, each of the four canonizers is also a SAT-solver.
φ and ψ. Then
| 1. | φ is valid |
iff | spdnf(φ) = true |
iff | spcnf(φ) = true |
| 2. | φ is satisfiable |
iff | spdnf(φ) ≠ false |
iff | spcnf(φ) ≠ false |
| 3. | φ => ψ |
iff | spdnf([φ -> ψ]) = true |
iff | spcnf([φ -> ψ]) = true |
| 4. | φ <=> ψ |
iff | spdnf([φ <-> ψ]) = true |
iff | spcnf([φ <-> ψ]) = true |
For example, [x + -x] is valid, because
$ ./PropLogic spcnf "[x + -x]" true
This concludes our introduction to the PropLogic command as a tool for propositional logic.
Note, that you can always call for immediate help from the command itself by typing
$ ./PropLogic help
If you do so, you will find that PropLogic has some more options we didn't cover, yet.
This involves just some more variations of the Prime Normal Form idea and we explain that in the next chapter.
The last chapter below then finally attempts to give an impression on the performance of the PropLogic command.
Therefore, it also has an option testing that generates a series of randomly generated forms, generates their canonizations and reports some measurements for the whole process.
There is yet another variation of the pdnf function, namely xpdnf. The "x" here simultaneously stands for "indexed" as well as "extended" [ThAlg].
Let us consider an example. First the PDNF
$ ./PropLogic pdnf "[x -> y -> z]" [[-x * -y] + [-x * z] + [y * z]]
then the XPDNF of the same formula
$ ./PropLogic xpdnf "[x -> y -> z]" +------------------+ | XPDNF | | +----+----+----+ | | | x | y | z | | | +----+----+----+ | | | -1 | -2 | | | | +----+----+----+ | | | -1 | | +3 | | | +----+----+----+ | | | | +2 | +3 | | | +----+----+----+ | +------------------+
It is easy to see that this table displays very much the same information than the PDNF. In the first row, there is the ordered lists of atoms: x, y, z. The other three rows are representations of the three NLCs of the PDNF, namely [-1,-2] stands for [-x * -y], [-1,3] stands for [-x * z], and [2,3] stands for [y * z].
The form is "indexed" in the sense that 1, 2, ... refer to the corresponding first, second, ... element in the ordered atom list, in this example case [x,y,z].
The output of the xpdnf call is a two-dimensional table display. The underlying data structure in Haskell for these XPDNFs has the following components:
The X-Form, here ([x,y,z],[[-1,-2],[-1,3],[2,3]], which is made of
The ordered atom list, here [x,y.z]
The I-Form, here [[-1,-2],[-1,3],[2,3]], which is a list of three I-Lines [-1,-2], [-1,3], and [2,3]
[COSTACK].
Each I-Line is a list [i_1, i_2, ..., i_n] of non-zero integers in an ordered fashion, namely abs(i_1) < abs(i_2) < ... < abs(i_n).
3. An indication (i.e. a type constructor in Haskell), here "XPDNF", that tells how the X-Form needs to be translated into a propositional formula.
In the example, the X-Form ([x,y,z],[[-1,-2],[-1,3],[2,3]] is supposed to be a XPDNF, so the X-Form translated into a formula is the DNF [[-x * -y] + [-x * z] + [y * z]]. If the X-Form would have been a XPCNF, then its conversion into a formula would have been the CNF [[-x + -y] * [-x + z] * [y + z]].
The deeper reason for these X-Forms is the gain in speed. The "fast" canonizers that do the real work under the surface translate propositional formulas into X-Forms, and by far the most work is done on the I-Forms. In particular, it involves a lot of atom comparisons, and it is much "cheaper" to work on integers than comparing arbitrary atoms, e.g. strings.
Yet another advantage of the X- and I-Form abstraction is the fact that each function can be applied twice, for DNFs and CNFS, due to the dual character of propositional logic.
An important example for the just mentioned exploitation of the dualism is the Haskell function
primForm :: IForm -> IForm
that takes an IForm q and returns its Prime Normal Form q'.
The DNF of q' is then the PDNF of the DNF of q, and the CNF of q' is the PCNF of the CNF of q.
This function can also be called from the command line with
$ ./PropLogic primForm IFORM
where IFORM is an I-Form, wrapped in double quote. For example,
$ ./PropLogic primForm "[[-1,2,3],[1,2,3],[-1,2,-3],[-1,-2,3],[-1,-2,3],[-1,2,3]]" [[-1,2],[-1,3],[2,3]]
And this result can be read in two dual versions:
[[-1 * 2] + [-1 * 3] + [2 * 3]] is the PDNF of the DNF
[[-1 * 2 * 3] + [1 * 2 * 3] + [-1 * 2 * -3] + [-1 * -2 * 3] + [-1 * -2 * 3] + [-1 * 2 * 3]]
[[-1 + 2] * [-1 + 3] * [2 + 3]] is the PCNF of the CNF
[[-1 + 2 + 3] * [1 + 2 + 3] * [-1 + 2 + -3] * [-1 + -2 + 3] * [-1 + -2 + 3] * [-1 + 2 + 3]]
The primForm function will probably not be very interesting for the normal user. But it is the core function of all the other prime canonizers and it does the most work behind the scenes. It therefore is the candidate we are going to study for the performance of our whole Prime Normal Form approach to propositional logic.
Generating Prime Normal Forms is a NP-hard problem [NP], we don't know if it can be done in polynomial time. Simply put, we don't know if there is a feasible algorithm for input of arbitrary size.
In this part we are going to present some empirical data on the computational costs of our primForm function.
The actual testing function generates random input for primForm according to certain size parameters, and measures how long primForm takes to produce the results.
This concentration on just one function may need some justification. After all, the propositional algebras we implemented in the PropLogic package consist of about thirty functions. A full performance study should check them all.
Besides, primForm works on I-Forms, but the average user would rather work with propositional formulas.
However, note that
most of the functions in the "fast" instances of propositional algebras are indeed of trivial or polynomial complexity. The harder ones, at least the theoretically harder ones, all use the prime form conversion, which does the essential and biggest part of the work.
There is also a function to produce random propositional formulas. But it turns out, that the majority of these formulas are extreme, i.e. either tautologies or contradictions. This is not a flaw of the random generator, but a property of the data structure itself. The prime normal forms of extreme formulas are produced more or less instantanuously. But we are interested in the difficult cases, and random I-Forms are much better material input, as we will see. Recall, that I-Forms are just abstractions of DNFs and CNFs, and that converting a formula into either a DNF or CNF can be done in polynomial time [POLY]. The real work comes when DNFs and CNFs are converted into their prime normal forms.
There is an infinite variety of NP-complete problems, but they are all related and the SAT solver or boolean satisfiability problem is a distinguished representative [SAT]. The primForm function is also a SAT solver and our data here is also designed to take part in the discussion about fast SAT solvers.
Recall, that this SAT solver works as follows:
Given an I-Form q and let q' := primForm(q) be the prime normal form of q.
If q is read as a DNF, then this DNF is
satisfiable iff q' is not [],
valid iff q' is [[]].
If q is read as a CNF, then this CNF is
satisfiable iff q' is not [[]],
valid iff q' is [].
For example, the primForm call and result
$ ./PropLogic primForm "[[-1,2,4],[1,4],[-3,4],[2],[-2,3]]" [[2],[3],[4]]
tell us that the DNF
[[-1 * 2 * 4] + [1 * 4] + [-3 * 4] + [* 2] + [-2 * 3]]
is satisfiable, but not valid, and that the CNF
[[-1 + 2 + 4] * [1 + 4] * [-3 + 4] * [+ 2] * [-2 + 3]]
is also satisfiable and not valid [SatLog].
We generate random I-Forms, apply primForm and then report the time that took. We do that many times, and thus obtain data for both the average and the worst case performance and we do all that with an average personal computer [Hardware].
Φ = [[i1,1,...,i1,n1],...,[im,1,...,im,nm]]
we define
atomNumber(Φ)X of the different 1,...,X occurring either positive or negativeformLength(Φ) := mvolume(Φ) := n1 + n2 + ... + nmaverageLineLength(Φ) := (n1+...+nm)/mFor example, the I-Form
[[-1,2,4],[1,4],[-3,4],[2],[-2,3]]
has the atoms 1,2,3,4, so the atom number is 4. The I-Form length is 5, the volume is 10 and the average I-Line length is 10/5=2.
The Haskell function for the random generation of I-Forms is [HAct]
randomIForm :: Int -> Int -> Int -> IO IForm
i.e. we call it with three integer arguments
randomIForm X Y Z
where X is the atom number, Y is the I-Form length, and Z is the average I-Line length.
For example, if we repeatedly call say
randomIForm 4 5 2
we obtain I-Forms like
[[-1,-3,4],[2,3],[-4],[-1,-2],[1,-3]] [[1,-3,-4],[-2,-4],[-1,2,3,-4],[1],[-4]] [[2,4],[-1,-4],[1,-4],[-2],[-2,-3,-4]] [[-2,-3],[1,-2],[-1,-2,3,4],[3,-4],[-1,2]] etc.
This random generator is not available from the command line directly. But it is part of the following testing function.
The testing function calls randomIForm a requested N number of times and has the syntax
PropLogic testing X Y Z N
where X is the atom number, Y the I-Form length, Z is the average I-Line length and N is the number of test trials.
If we call e.g.
$ ./PropLogic testing 4 5 2 1000
we finally obtain something like this [Verbose]
+----------------------------------------------------------+ | All 1000 tests have been performed: | | Parameters for the random IForms were: | | atomNumber = 4 | | formLength = 5 | | averageLineLength = 2 | | Result of the test series: | | numberOfTests = 1000 | | maxFormLength = 9 | | averageFormLength = 2 | | maxTime = 4.001e-3 seconds | | averageTime = 1.6801500000000012e-4 seconds | | standardTimeDeviation = 8.024281742156195e-4 seconds | +----------------------------------------------------------+
Obviously, this description first recalls the input parameters and then displays the the result of the test series, namely:
the numberOfTests again, which was the input 1000, and then the measurements for the worst (maximal) and the average results of the primForm conversion.
More precisely, if the N random forms were p_1,...,p_N, if q_1,...q_N are the according results, i.e. q_i=primForm(p_i), and if this would have been obtained in t_1,...,t_N seconds, respectively, then the test result would show:
numberOfTests = N
maxFormLength = max { formLength(q_1), ..., formLength(q_N) }
averageFormLength = (formLength(q_1) + ... + formLength(q_N)) / N
maxTime = max { t_1, ..., t_N }
averageTime = (t_1 + ... + t_N) / N
standardTimeDeviation = ((averageTime - t_1)^2 + ... + (averageTime - t_N)^2) / N
The computational complexity, i.e. the performance of an algorithm is usually expressed as a functional dependency of the time and space recources from the size of the input. The input of the primForm function is an I-Form. But we already have different notions to express the size of an I-Form: atomNumber, formLength, averageLineLength and volume. So which one is it?
Actually, one might argue that volume is the "real" size measure. But in fact, as we are going to demonstrate below, it is not the most suitable one for an analysis of the situtation we consider. From a theoretical point of view, the atomNumber is in fact the real parameter that expresses the complexity of the problem, and this is also the predominant one in the literature on complexity theory. However, given an atom number X, it does make a huge performance difference which length Y and average I-Line length Z we choose when we run PropLogic testing X Y Z N.
Let us now run our testing function by calling
$ ./PropLogic testing X Y Z N
where X is the atomNumber, Y is the formLength and Z is the averageLineLength of the N randomly generated I-Forms.
But instead of simply accumulating data, let us establish some facts about the general performance behaviour of the primForm function.
Calling
$ ./PropLogic testing 5 10 4 1000
gave us the final result
+-----------------------------------------------------------+ | All 1000 tests have been performed: | | Parameters for the random IForms were: | | atomNumber = 5 | | formLength = 10 | | averageLineLength = 4 | | Result of the test series: | | numberOfTests = 1000 | | maxFormLength = 17 | | averageFormLength = 8 | | maxTime = 2.0002e-2 seconds | | averageTime = 2.3721570000000006e-3 seconds | | standardTimeDeviation = 2.6394240520141716e-3 seconds | +-----------------------------------------------------------+
Recall, that this means: we generated 1000 random I-Forms p_1,...,p_1000 of length 10, average I-Line length 4, and thus a volume of approximately 10*4=40. For each of those I-Forms, the Prime Normal Form q_i=primForm(p_i) was computed in t_i seconds. The maximal length of all these p_1,...,p_1000 was 17, the average length was 8. The maximal time of the t_1,...,t_1000 was about 20 milli-seconds, the average time was around 2 milli-seconds with an standard deviation of about 2 milli-seconds as well.
This example already reveals a general phenomenon: although the Prime Normal Forms q_i are most of the time shorter than the original I-Form p_i, in this case an average length of 8 compare to the length 10 of p_i, it may as well become longer, namely up to 17 in the given test trail.
In other words, Prime Normal Form and Minimal Normal Form are different, most of the time!
Actually, if q = [l_1,...,l_k] is a Prime Normal Form, an equivalent Minimal Normal Form q' = [m_1,...,m_h] is a selection of the I-Lines of q, i.e. {m_1,...,m_h} is a subset of {l_1,...,l_k}.
For example, [[1,2],[1,3],[2,-3]] is a Prime Normal Form and [[1,3],[2,-3]] is an equivalent Minimal Normal Form.
Well, if there are indeed Minimal Normal Forms, why are we not using them as standard canonizations, instead of the Prime Normal Forms? A full discussion and answer is given in [PNFCanon], but two crucial arguments are: 1. Minimal Normal Forms are not unique in general, there may be several equivalent ones, and 2. for the generation of Minimal Normal Forms it seems to be necessary to generate the Prime Normal Forms, so that their is neither a reduction of space, nor a reduction of time in the process.
If all other parameters stay the same, the increase of the formLength increases the costs considerably.
For example, if we keep
atomNumber = averageLineLength = 10
then a variation of the formLength produced the following results:
formLength | maxFormLength averageFormLength maxTime averageTime
===========+=======================================================
10 | 10 9 0.064 0.001
100 | 87 77 0.248 0.148
500 | 452 403 91.9 56.1
1000 | 877 795 1659 1258
Note in particular, that a length increase from 10 to 1000 results in a time increase from milli-seconds to almost half an hour.
Nevertheless, this increasing tendency is only local. From a certain point onwards, a further increase of the length results in smaller Prime Normal Forms. Recall, that for an atom number of X, there are only 2^X different I-Lines of length X. The more I-Lines we add, the greater is the chance that the I-Forms collapses into the unit Prime Normal Form.
To demonstrate that, let us use an atomNumber of 4, i.e. we run
$ ./PropLogic testing 4 Y 4 10000
for different formLength=Y. The following graph shows the decline of both the maximal and the average I-Form length of the Prime Normal Forms after a peak for around formLength=14.
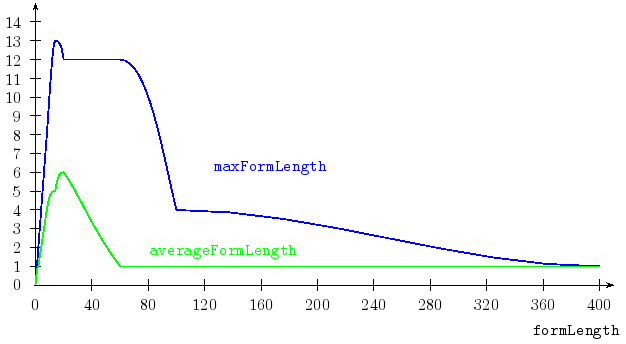
A high atomNumber alone doesn't make problems unfeasible.
For example, let us take
atomNumber = 1000
Some examples for a relatively small formLength (with averageLineLength set to 500 and N=100 tests) are:
formLength | maxFormLength averageFormLength maxTime averageTime
===========+=====================================================
10 | 10 10 0.036 0.006
50 | 50 50 0.304 0.092
500 | 500 500 10.35 9.1
2000 | 2000 2000 308.7 304.3
As we may suggest from the values of maxFormLength and averageFormLength, the input form is hardly changed, i.e. the random I-Forms are already in Prime Normal Form, but we don't care about a detailed explanation here.
For an atomNumber of 1000 however, there are I-Forms with <formLength 2^1000> where all I-Lines are different and the Prime Normal Forms are not much smaller either [PrimNum], and that is beyond any limits we can hope for here.
The following test shall try to reveal the worst case behavior for a given atomNumber=X. We put
formLength := 2^X averageLineLength := X
and slowly increase X. We obtain
atomNumber formLength averageLineLength numberOfTests | maxFormLength maxTime
X 2^X X N |
=======================================================+=========================
2 4 2 1000 | 2 0.004
3 8 3 1000 | 6 0.004
4 16 4 1000 | 13 0.008
5 32 5 1000 | 24 0.056
6 64 6 1000 | 46 0.28
7 128 7 1000 | 92 2.2
8 256 8 1000 | 193 18.0
9 512 9 200 | 419 245
10 1024 10 5 | 833 2970
If we use an average equipment and if we accept a maximal waiting time up to say one minute, then the Prime Normal Form canonization is feasible for input forms with an atom number of 8.
The compiled function
PropLogic testing X Y Z N
is the renamed version of the Haskell function verboseRandomPrimeTesting, which is called from within the ghci interpreter as
verboseRandomPrimeTesting (X,Y,Z) N
Running some tests showed that the interpreted version is only about 15% slower.
http://www.bucephalus.org/text/InstallPropLogic/InstallPropLogic.html
is a more detailed description of the installation and setup of the PropLogic package.
If you are not familiar with Haskell, the function signature such as
pdnf :: (Ord a) => PropForm a -> PDNF a
probably looks awkward. But it is what more conventional mathematicians would rather write as
pdnf : PropForm(a) -> PDNF(a)
i.e. the function pdnf has the propositional formulas on the parametric atom type a as its domain and the PDNFs on a as its codomain. In Haskell, the type operator ":" is written "::" (because ":" is reserved for list construction; "x:l" is the same as "(cons x l)" in LISP). The prefix (Ord a) => means that this function is only defined on an atom type a that has a (linear) order structure defined on it.
(This is an example of the type class concept, which is a pretty unique Haskell feature.)
The rules for the simplification are the following ones.
[*] <=> true[+] <=> false[* φ] <=> φ[+ φ] <=> φ[φ1 * ... * φm * true * ψ1 * ... * ψn] <=> [φ1 * ... * φm * ψ1 * ... * ψn][φ1 + ... + φm + true + ψ1 + ... + ψn] <=> true[φ1 * ... * φm * false * ψ1 * ... * ψn] <=> false[φ1 + ... + φm + false + ψ1 + ... + ψn] <=> [φ1 + ... + φm + ψ1 + ... + ψn]In the Haskell implementation, the built-in Haskell lists are replaced by so-called costacks, i.e. I-Lines are costacks of integers and I-Forms are costacks of I-Lines.
Functional programming languages with LISP as a common ancestor implement lists as stacks, i.e. lists can only be modified by adding or removing a head component. Therefore, the concatenation of two lists is not a primitive operation, one first needs to walk throught the entire first list to then attach the second one. A costack or concatenable stack therefore is a list-like data structure, where concatenation is indeed a primitive operation, too.
The "fast" normalizers in the PropLogic package do their main work on I-Lines and I-Forms, and they do apply concatenations frequently. Therefore, the costack data structure is implemented in a separate Costack module.
(In fact however, the real implementation of costacks in the Costack module is currently still done with ordinary Haskell lists. Different, more effective implementations are intended for future releases of the PropLogic package.)
In this introduction, we only concentrate on the "indexed" interpretation of the "X", i.e. how the atoms are replaced by positive integers to make the data structures more efficient. We neglect the "extended" meaning of the "X". On a deeper level, this very much has to do with our theory-algebraic reconstruction of propositional logic in favor of the traditional algebraization as a boolean algebra (see the other literature on http://www.bucephalus.org/PropLogic).
But also in the use of the command line, it shows us that the XPDNF is not just a another representation of the PDNF, but carries a little more information. Consider the formula [x -> y -> [z + true]]. The atom z is what we call redundant in the formula in the sense that there are equivalent formulas without z. Prime Normal Forms only contain irredundant atoms and we see that z is disappeared in the PDNF
$ ./PropLogic pdnf "[x -> y -> [z + true]]" [[* -x] + [* y]]
But the XPDNF preserves all the atoms, it is equiatomic to the original formula
$ ./PropLogic xpdnf "[x -> y -> [z + true]]" +-----------------+ | XPDNF | | +----+----+---+ | | | x | y | z | | | +----+----+---+ | | | -1 | | | | | +----+----+---+ | | | | +2 | | | | +----+----+---+ | +-----------------+
and it is not just
+-------------+ | XPDNF | | +----+----+ | | | x | y | | | +----+----+ | | | -1 | | | | +----+----+ | | | | +2 | | | +----+----+ | +-------------+
see e.g. http://en.wikipedia.org/P_versus_NP_problem for an introduction into the discussion in complexity theory.
Actuall, that the DNF and CNF conversion of propositional formulas can be done in polynomial time, is a questionable statement. At least for our special versions of propositional formulas, that also allow sub- and equijunctions. But this is not the main focus in complexity theory and we ignore the possible objections here. Besides, in the "fast" instances of propositional algebras in the PropLogic package are all based on data structures, where propositions are represented as DNFs or CNFs of some sort.
There are online discussions devoted to the SAT problem, e.g. http://www.satlive.org and http://www.satisfiability.org.
In fact, the test for the satisfiability of a DNF (and the test for the validity of the CNF) are trivial: Due to the semi-ordered definition of our DNFs, every DNF other than [+] is satisfiable anyway, because if it has at least one NLC [L1 * ... * Lm], then this NLC is satisfiable (because the L1,...,Lm cannot contain a complementary pair of literals), and so is the disjunction of multiple NLCs. So in fact, the satisfiability test is really only significant for CNF interpretations of I-Forms. But that doesn't change the general argument.
Intel Pentium Dual CPU, 1.60 GHz; 2GB memory; Ubuntu Linux 8.10; Glasgow Haskell Compiler, Version 6.10.4.
A call of the testing function produces very verbose output, for each of the N test cases it reports the full situation. This is done because when the random formulas become bigger, each primForm call becomes harder to perform and running test series may take long periods of time where nothing happens and a verbose version gives a better feeling for the behavior. On the other hand, this output-production adds to the time which is measured. But we neglect this artificial brake on the speed.
The Haskell type expression
randomIForm :: Int -> Int -> Int -> IO IForm
shows two more typical features of common Haskell functions: the three arguments are not given as a triple, the domain of the function is not a ternary cartesian product. The function is "currified" into a higher-order function of third degree.
And the type IO IForm is the type of "actions" on I-Forms, encapsulated in IO to preserve the purely functional character of the language. Otherwise, randomIForm wouldn't be a proper function, because the result is not deterministic; typical for a random generator. (The theoretical framework for all this is the famous "monad" concept of Haskell.)
http://www.bucephalus.org/text/PNFCanon/PNFCanon.html
The 36 pages paper called
Theory and implementation of efficient canonical systems for sentential calculus, based on Prime Normal Forms
is the main source for the mathematical background of the approach and algorithms in the PropLogic package.
There are studies on the length of Prime Normal Forms, such as: A. K. Chandra, George Markowsky: On the Number of Prime Implicants, Discrete Mathematics 24 (1978), p.7-11, (http://laptops.maine.edu/NumPrimeImplicants.pdf).