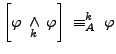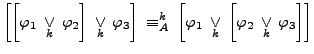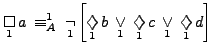bucephalus.org

Algebraic properties of hyper-digital logic

online since July 2007

Abstract

Having defined the syntax and semantics of hyper-digital logic (see [1]), this paper investigates the basic properties of the quasi-order relation on hyper-propositional formulas of a given carrier set A and degree k.

One set of properties immediately derives from the fact that these formula algebras are quasi-boolean algebras. We for example have

the idempotency of conjunctions:
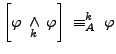
the associativity of disjunctions:
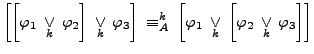
the law of double negation:

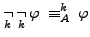
Another set of properties involves the "box" and "diamond" operators and many results are similar to axioms and theorems of modal logic, such as

the duality of box and diamond:

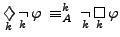
But not all phenomena fit into the perspective of traditional logical systems:

If say is the carrier set then
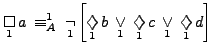
Let S and T be two carrier sets, S a subset of T. In traditional propositional logic, we can always increase the carrier set at any time in the sense that 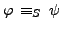always implies 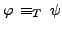. But this is no longer true in hyper-propositional logic, where for each degree k there are two formulas with 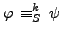and .

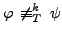From a deeper point of understanding of course, these "surprising" phenomena turn into perfectly normal behaviour.

The text

The full text is currently under construction.

References

[1] Hyper-digital logic: Summarized overview of its syntax and semantics

Algebraic properties of hyper-digital logic

Abstract

The text

References

[home] [blog]